
Sliding Window and Two Pointer Technique (Photo Credit: Google Image)
Story
There is a school called ABC School, which frequently arranges extracurricular activities like games, dancing competitions, art competitions, etc. for their students. Today it arranged 2 interesting games called sliding window and rope pulling.
The rules for the sliding window game are: first, make 2 teams; second, each team takes their position, and then, based on some condition, they slide their window 1 or more units until the window reaches the end position.
The rules for the rope-pulling game are almost similar to those for the sliding window, and that is: first, make 2 teams; second, each team takes their position, and then they start pulling the rope. As a result, the team that has more strength than the other pulls the other team to their area, and the team with less strength comes to the other team’s area. The game finishes when one team enters the other team’s area.
Sliding Window Technique
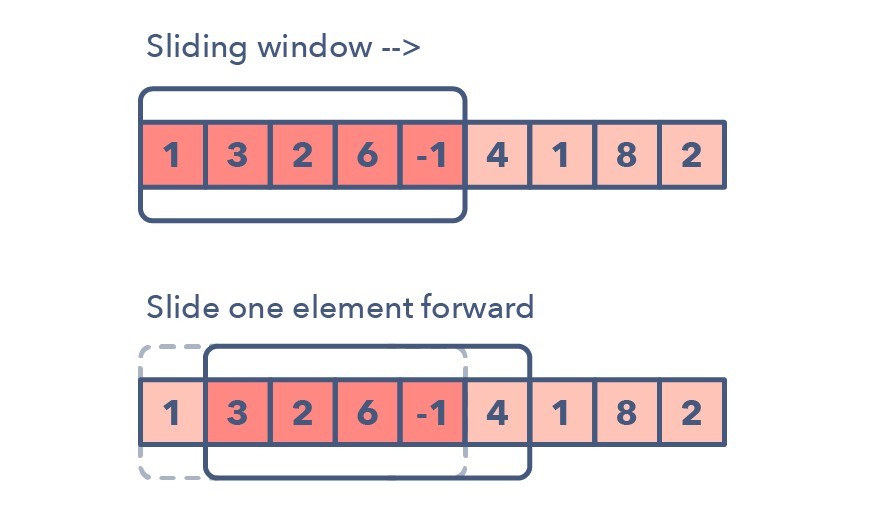
Sliding Window Technique (Photo Credit: Towards Dev)
The Window Sliding technique is a computational technique that aims to reduce the use of nested loops and replace them with a single loop, thereby reducing the time complexity. In this technique, we reuse the result of the previous step to compute the result of the next step. It is a problem-solving technique of data structure and algorithm for problems that apply arrays or lists. These problems are painless to solve using a brute force approach in O(n²) or O(n³). However, the sliding window technique can reduce the time complexity to O(n). So the main idea behind the sliding window technique is to convert two nested loops into a single loop.
In the above story, the sliding window game works like our sliding window algorithm. There window has two points and a fixed size, and it slides until the end point arrives.
Basic Steps to Solve Sliding Window Problems:
- Find the size of the window on which the algorithm has to be performed.
- Calculate the result of the first window, as we calculate in the naive approach.
- Maintain a pointer on the start position.
- Then run a loop and keep sliding the window by one step at a time and also sliding that pointer one at a time, and keep track of the results of every window.
Typical use cases:
Used when you want to examine a contiguous block (window) of elements in an array/string.
- Longest substring without repeating characters
- Maximum sum of a subarray of size
k - Minimum size subarray sum ≥
target
Pseudocode (Fixed Size Window)
| |
Pseudocode (Variable Size Window)
| |
Two Pointer Technique

Two Pointer Technique (Photo Credit: Vector Stock)
Like the name suggests, two pointers work using 2 pointers, or positions of data structures, ideally lists/arrays. It is an excellent technique for working with pairs, separating data, finding ranges (or subsequences) in sequences, or even finding a cycle in a linked list. It compares the values of 2 positions or pointers. It is a pattern in which two pointers iterate across the data structure until one or both of them satisfy the necessary condition.
In the above story, the rope-pulling game works kind of similarly to our two-pointer technique. Where two teams act like two pointers, and they start moving their position based on force (which can be considered a condition of the 2-pointer technique), and this works until 1 team crosses their area.
Basic Steps to Solve Two-Pointer Problems:
- Pointer initialization: First initialize the pointer positions based on the problem criteria.
- Pointer movement: Move the pointers based on the condition check of either the 1st pointer or the second pointer or both.
- Stop condition: Identify and apply the stop condition based on the problem expectation.
Typical use cases:
Used for non-contiguous elements or sorted arrays, often to find pairs or perform merging.
- Two sum in sorted array
- Remove duplicates
- Merging sorted arrays
- Trapping rainwater
Pseudocode
Difference Between Sliding window and Two Pointer Technique:
- Sliding window algorithms can be implemented with a single pointer and a variable for window size. Typically we use all of the elements within the window for the problem (for example, the sum of all elements in the window).
- The two-pointer technique is quite similar, but we usually compare the value at the two pointers instead of all the elements between the pointers.
| Feature | Sliding Window | Two Pointer |
|---|---|---|
| Works on | Contiguous subarrays/strings | Sorted arrays / general arrays |
| Pointer direction | Usually one moves (start/end) | Both pointers move toward each other |
| Window size | Fixed or dynamic | No “window”, but two indices |
Problems Can Be Solved
Using sliding window:
- Substring with Concatenation of All Words
- Find All Anagrams in a String
- Permutation in String
- Maximum Average SubarrayI
- Longest Substring Without Repeating Characters
- Minimum Window Substring
- Longest Substring with At Most Two Distinct Characters
- Minimum Size Subarray Sum
Using two pointer technique: